 Home Page
Home Page
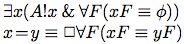
The equations at the top of this page are the two most important principles of the theory of abstract objects. The first principle expresses the existence conditions for abstract objects; the second expresses their identity conditions. In this document, we try to give you some idea of what these principles say.
The theory of abstract objects is a metaphysical theory. Whereas physics attempts a systematic description of fundamental and complex concrete objects, metaphysics attempts a systematic description of fundamental and complex abstract objects. Abstract objects are the objects that are presupposed by our scientific conceptual framework. For example, when doing natural science, we presuppose that we can use the natural numbers to count concrete objects, and that we can use the real numbers to measure them in various ways. It is part of our understanding of science that natural laws exist (even if no one were around to discover them) and that the states of affairs that obtain in the natural world are governed by such laws. As part of our scientific investigations, we presuppose that objects behave in certain ways because they have certain properties, and that natural laws govern not just actual objects that have certain properties, but any physically possible object having those properties. So metaphysics investigates numbers, laws, properties, possibilities, etc., as entities in their own right, since they seem to be presupposed by our very understanding of the scientific enterprise. The theory of abstract objects attempts to organize these objects within a systematic and axiomatic framework.
It would be a mistake to think that a theory postulating abstract objects is incompatible with our theories of natural science, which seem to presuppose that the only things that exist are the things governed by our true scientific theories. To see that the theory of abstract objects is compatible with natural scientific theories, we only have to think of abstract objects as possible and actual property-patterns. These patterns of properties objectify a group of properties that satisfy a certain pattern. For example, it will turn out that the real number π can be thought of as the pattern of properties satisfying the open sentence "According to the axioms of real number theory, π has the property F" (where "F" is a variable ranging over properties). There are an infinite number of properties satisfying this pattern (and an infinite number that don't). Our theory of abstract objects will "objectify" or "reify" the group of properties satisfying this pattern. So, on this view of what abstract objects are, we need not think of them as some ghostly, imperceptible kind of nonspatiotemporal substances. Instead, they are possible and actual patterns that are grounded in the arrangement of particles in the natural world and in the systematic behavior and linguistic usage of mathematicians and scientists as they discover, state, and apply theories of the natural world.
We can summarize the principal objectives of the theory of abstract objects as follows:
Further Explanation of the Objectives of the Theory
The Distinction Underlying the Theory
The theory is based on Ernst Mally's distinction between exemplifying and encoding a property. This is a distinction between two fundamental kinds of predication, and it is formally represented in the theory as the distinction between the atomic formulas ‘Fx’ (‘x exemplifies F’) and ‘xF ’ (‘x encodes F’). The formula ‘Fx’ represents the classical kind of predication; it is used to logically analyze such simple sentences as ‘John is happy’, ‘Clinton is president’, and ‘Socks is a cat’. Mally's idea, in essence, was that we should not represent sentences about fictional objects, such as ‘Sherlock Holmes is a detective’, ‘Pegasus has wings’, ‘King Lear had 3 daughters’, and ‘Zeus lived on Mt. Olympus’, in terms of the notation ‘Fx’ (only real, concrete objects can exemplify the properties of being a detective, having wings, having daughters, or living on Mt. Olympus). Nevertheless, Mally reasoned in effect that there must be some mode of predication, some sense of the words ‘is’ and ‘has’ (German ‘ist’ and ‘hat’), for which it is true to say ‘Sherlock Holmes is a detective’ and ‘Pegasus has wings’ (we wouldn't understand the story and myth properly if we didn't imagine objects that, in some sense, were instances of the properties in question).
So Mally informally introduced the notion ‘x encodes F’ (German: F determiniert x) as a new mode of predication that is more appropriate for the logical analysis of sentences about fictions and other abstract objects. Whereas the real detective Pinkerton exemplifies detectivehood (‘Dp’), Sherlock Holmes encodes this property (‘hD’). Mally's ideas can be extended to other abstract objects, such as numbers, sets, possible worlds, etc. Whereas we can identify and individuate concrete objects in terms of their spatiotemporal location, we must identify and individuate abstract objects in some other way, for abstract objects are not the kind of thing that could have a location in spacetime. Encoding provides the means of identifying and individuating abstract objects. The properties that an abstract object encodes are part of its intrinsic nature---they are even more essential to it than the properties that such objects exemplify necessarily.
Further Explanation of the Distinction Underlying the Theory
To extend Mally's idea to its logical conclusion, therefore, we simply assert the following two principles:
Though the theory of abstract objects has been presented in books and articles, there is one unpublished source in which all the theorems of the theory are compiled in one place. This is the monograph entitled Principia Logico-Metaphysica. It contains just the formal machinery, axioms, and theorems of the theory with very little accompanying explanation. It exists on-line in HTML, DVI (device independent), compressed PS (PostScript), and compressed PDF (Adobe Acrobat) file formats, and so can be examined with a graphical web browser, DVI file previewer, PS printer, or Adobe Acrobat reader. Since the manuscript contains little supporting explanation of the formal machinery, it will appear highly technical. However, there is help available for understanding the formal machinery, in the form of a Tutorial (see below).
Streaming Video Presentation of the Theory
"Steps Toward a Computational Metaphysics", by Edward N. Zalta and Branden Fitelson, Computing and Philosophy Conference, Oregon State University, August 8, 2003
 PDF (3.5 MB) (current version)
PDF (3.5 MB) (current version)
Tutorial on Principia Logico-Metaphysica
This tutorial assumes either: (1) that you have a multi-window graphical web browser that can display the HTML version of Principia Logico-Metaphysica in one window and display the tutorial in another other window, or (2) that your graphical web browser is supported with a DVI, PS, or Acrobat previewer and that you are able to flip back and forth between the (DVI, PS, or Acrobat) version of Principia Logico-Metaphysica in your previewer and the tutorial in your graphical web browser.
Tutorial